Math/basic
<Math |
Contents
Introduction
To tell TeX that an expression needs to be typeset using conventions for math, type the expression in $...$. For examples $x$ gives
 , while
, while $2$ gives 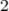 . Notice that the x is in italic while the 2 is upright. This is the usual mathematic convention. You can also write in the math mode using the commands \m, \math or \mathematics.
. Notice that the x is in italic while the 2 is upright. This is the usual mathematic convention. You can also write in the math mode using the commands \m, \math or \mathematics.
Thus, the following four are equivalent. Use the style that you prefer.
Pythagoras formula, stating $a^2 + b^2 = c^2$ was one of the first trigonometric results
Pythagoras formula, stating \m{a^2 + b^2 = c^2} was one of the first trigonometric results
Pythagoras formula, stating \math{a^2 + b^2 = c^2} was one of the first trigonometric results
Pythagoras formula, stating \mathematics{a^2 + b^2 = c^2} was one of the first trigonometric results
and gives
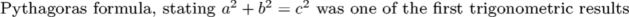
Binary Operators Relations
Basic binary symbols can be produced by typing the correspoding keyboard character. These include
+ - = < >
A general expressions can be input in the natural manner. For example $x+y$ gives 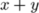 . Notice that TeX took care of the spacing around
. Notice that TeX took care of the spacing around +. Mathematicians use a lot of symbols that are not avialable on the keyboard. TeX (and ConTeXt) provide macros to input them. For example $x \times y$ gives 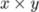 . The following is a parial list of frequently used binary operators and relations.
. The following is a parial list of frequently used binary operators and relations.
| Commonly Used Binary Operators | Commonly used relation symbols | Set Relations | |||
|---|---|---|---|---|---|
| \pm | 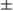
|
\leq | 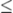
|
\subset | 
|
| \mp | 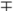
|
\ll | 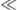
|
\subseteq | 
|
| \times | 
|
\geq | 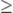
|
\supset | 
|
| \div | 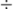
|
\gg | 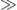
|
\supseteq | 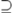
|
| \ast | 
|
\equiv | 
|
\cap | 
|
| \star | 
|
\sim | 
|
\cup | 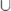
|
| \bullet | 
|
\simeq | 
|
\in |
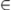
|
| \circ | 
|
\approx | 
| ||
| \cdot | 
|
\neq | 
| ||
Greek Letters
To type the greek character α you can say $\alpha$ which gives  . If you have a utf enabled keyboard, you can also type the α directly and ConTeXt will correctly interpret it. For example,
. If you have a utf enabled keyboard, you can also type the α directly and ConTeXt will correctly interpret it. For example,
\enableregime[utf] Here is some Greek math $α^2 + β^2 = γ^2$
Here is a complete list of greek letters
| lowercase greek letters | variation | uppercase greek letters | |||
|---|---|---|---|---|---|
| \alpha | 
| ||||
| \beta | 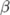
| ||||
| \gamma | 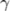
|
\Gamma | 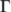
| ||
| \delta | 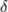
|
\Delta | 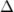
| ||
| \epsilon | 
|
\varepsilon | 
| ||
| \zeta | 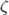
| ||||
| \eta | 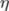
| ||||
| \theta | 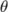
|
\vartheta | 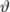
|
\Theta | 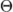
|
| \iota | 
| ||||
| \kappa | 
| ||||
| \lambda | 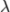
|
\Lambda | 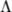
| ||
| \mu | 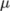
| ||||
| \nu | 
| ||||
| \xi | 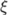
|
\Xi | 
| ||
| \omicron | 
| ||||
| \pi | 
|
\varpi | 
|
\Pi | 
|
| \rho | 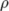
|
\varrho | 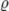
| ||
| \sigma | 
|
\varsigma | 
|
\Sigma | 
|
| \tau | 
| ||||
| \upsilon | 
|
\Upsilon | 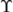
| ||
| \phi | 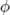
|
\Phi | 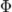
| ||
| \chi | 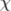
| ||||
| \psi | 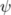
|
\Psi | 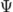
| ||
| \omega | 
|
\Omega | 
| ||
subscript and superscipt
TeX uses ^ and _ to denote superscipts and subscipts. It is perhaps easiest to explain this by means of some examples. 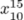 is written as
is written as $x_{10}^{15}$ or $x^{15}_{10}$. The order in which _ and ^ are given does not matter. One can also type complicated expressions like  as
as $a_{b_{c_{d_{e}}}}$.
To align superscripts and subscripts one after the other (not above/below each other), add empty braces {} after each of them as $T^a{}_b{}^c{}$ to obtain 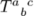 . This effectively adds each index as superscript/subscript of the empty braces rather than the main character, thus aligning them separately and avoiding double superscript errors.
. This effectively adds each index as superscript/subscript of the empty braces rather than the main character, thus aligning them separately and avoiding double superscript errors.
List of All Math macros
In ConTeXt MkII, you can see the list of all math macros by \showmathcharacters. In MkIV, \usemodule[fnt-25] followed by \showmathfontcharacters produces a lengthy annotated catalogue.
Here is the first page of this list