Programming in LuaTeX
 |
NOTE: This is a wikified version of this TugBoat article . Feel free to modify it. |
In this article, I explain how to use lua to write macros in LuaTeX. I give some examples of macros that are complicated in PdfTeX, but can be defined easily using lua in luaTeX. These examples include macros that do arithmetic on their arguments, use loops, and parse their arguments.
Contents
Introduction
TeX is getting a new engine—luaTeX. As its name suggests, luaTeX adds lua, a programming language, to TeX, the typesetter. I cannot overemphasize the significance of being able to program TeX in a high-level programming language. For example, consider a TeX macro that divides two numbers. Such a macro is provided by the fp package and also by pgfmath library of the TikZ package. The following comment is from the fp package
\def\FP@div#1#2.#3.#4\relax#5.#6.#7\relax{% % [...] algorithmic idea (for x>0, y>0) % - %determine \FP@shift such that % y*10^\FP@shift < 100000000 % <=y*10^(\FP@shift+1) % - %determine \FP@shift' such that % x*10^\FP@shift'< 100000000 % <=x*10^(\FP@shift+1) % - x=x*\FP@shift' % - y=y*\FP@shift % - \FP@shift=\FP@shift-\FP@shift' % - res=0 % - while y>0 %fixed-point representation! % - \FP@times=0 % - while x>y % - \FP@times=\FP@times+1 % - x=x-y % - end % - y=y/10 % - res=10*res+\FP@times/1000000000 % - end % - %shift the result according to \FP@shift
The pgfmath library implements the macro in a similar way, but limits the number of shifts that it does. These macros highlight the state of affairs in writing TeX macros. Even simple things like multiplying two numbers are hard; you either have to work extremely hard to circumvent the programming limitations of TeX, or, more frequently, hope that someone else has done the hard work for you. In luaTeX, such a function can be written using the / operator (I will explain the details later):
\def\DIVIDE#1#2{\directlua{tex.print(#1/#2)}}
Thus, with luaTeX ordinary users can write simple macros; and, perhaps more importantly, can read and understand macros written by TeX wizards.
Since the luaTeX project started it has been actively supported by ConTeXt. [1] These days, the various How do I write such a macro questions on the ConTeXt mailing list are answered by a solution that uses lua. I present a few such examples in this article. I have deliberately avoided examples about fonts and non-Latin languages. There is already quite a bit of documentation about them. In this article, I want to highlight how to use luaTeX to write macros that require some flow control: randomized outputs, loops, and parsing.
Interaction between TeX and lua
To a first approximation, the interaction between TeX and lua is straightforward. When TeX (i.e., the luaTeX engine) starts, it loads the input file in memory and processes it token by token. When TeX encounters \directlua, it stops reading the file in memory, {\em fully expands the argument of\/ \directlua}, and passes the control to a lua instance. The lua instance, which runs with a few preloaded libraries, processes the expanded arguments of \directlua. This lua instance has a special output stream which can be accessed using tex.print(...). The function tex.print(...) is just like the lua function print(...) except that tex.print(...) prints to a TeX stream rather than to the standard output. When the lua instance finishes processing its input, it passes the contents of the TeX stream back to TeX.[2] TeX then inserts the contents of the TeX stream at the current location of the file that it was reading; expands the contents of the TeX stream; and continues. If TeX encounters another \directlua, the above process is repeated.
As an exercise, imagine what happens when the following input is processed by luaTeX. [3]
\directlua% {tex.print("Depth 1 \\directlua{tex.print('Depth 2')}")}
On top of these luaTeX primitives, ConTeXt provides a higher level interface. There are two ways to call lua from ConTeXt. The first is a macro \ctxlua (read as ConTeXt lua), which is similar to \directlua. (Aside: It is possible to run the lua instance under different name spaces. \ctxlua is the default name space; other name spaces are explained later.) \ctxlua is good for calling small snippets of lua. The argument of \ctxlua is parsed under normal TeX catcodes (category codes), so the end of line character has the same catcode as a space. This can lead to surprises. For example, if you try to use a lua comment, everything after the comment gets ignored.
\ctxlua {-- A lua comment tex.print("This is not printed")}
This can be avoided by using a TeX comment instead of a lua comment. However, working under normal TeX catcodes poses a bigger problem: special TeX characters like \letterampersand, \letterhash, \letterdollar, \{, \}, etc., need to be escaped. For example, \letterhash\ has to be escaped with \string to be used in \ctxlua.
\ctxlua {local t = {1,2,3,4} tex.print("length " .. \string#t)}
As the argument of \ctxlua is fully expanded, escaping characters can sometimes be tricky. To circumvent this problem, ConTeXt defines a environment called \startluacode ... \stopluacode. This sets the catcodes to what one would expect in lua. Basically only \ has its usual TeX meaning, the catcode of everything else is set to other. So, for all practical purposes, we can forget about catcodes inside \startluacode ... \stopluacode. The above two examples can be written as
\startluacode -- A lua comment tex.print("This is printed.") local t = {1,2,3,4} tex.print("length " .. #t) \stopluacode
This environment is meant for moderately sized code snippets. For longer lua code, it is more convenient to write the code in a separate lua file and then load it using lua's dofile(...) function.
ConTeXt also provides a lua function to conveniently write to the TeX stream. The function is called context(...) and it is equivalent to tex.print(string.format(...)).
Using the above, it is easy to define TeX macros that pass control to lua, do some processing in lua, and then pass the result back to TeX. For example, a macro to convert a decimal number to hexadecimal can be written simply, by asking lua to do the conversion.
\def\TOHEX#1{\ctxlua{context("\%X",#1)}} \TOHEX{35}
The percent sign had to be escaped because \ctxlua assumes TeX catcodes. Sometimes, escaping arguments can be difficult; instead, it can be easier to define a lua function inside \startluacode ... \stopluacode and call it using \ctxlua. For example, a macro that takes a comma separated list of strings and prints a random item can be written as
\startluacode userdata = userdata or {} math.randomseed( os.time() ) function userdata.random(...) context(arg[math.random(1, #arg)]) end \stopluacode \def\CHOOSERANDOM#1% {\ctxlua{userdata.random(#1)}} \CHOOSERANDOM{"one", "two", "three"}
I could have written a wrapper so that the function takes a list of words and chooses a random word among them. For an example of such a conversion, see the sorting a list of tokens page on the Sort_a_token_list luaTeX wiki
In the above, I created a name space called userdata and defined the function random in that name space. Using a name space avoids clashes with the lua functions defined in luaTeX and ConTeXt.
In order to avoid name clashes, ConTeXt also defines independent name spaces of lua instances. They are
| user | a private user instance |
| third | third party module instance |
| module | ConTeXt module instance |
| isolated | an isolated instance |
Thus, for example, instead of \ctxlua and \type{\startluacode ... \stopluacode}, the user instance can be accessed via the macros \usercode and \startusercode ... \stopusercode. In instances other than isolated, all the lua functions defined by ConTeXt (but not the inbuilt lua functions) are stored in a global name space. In the isolated instance, all lua functions defined by ConTeXt are hidden and cannot be accessed. Using these instances, we could write the above \CHOOSERANDOM macro as follows
\startusercode math.randomseed( global.os.time() ) function random(...) global.context(arg[math.random(1, #arg)]) end \stopusercode \def\CHOOSERANDOM#1% {\usercode{random(#1)}}
Since I defined the function random in the user instance of lua, I did not bother to use a separate name space for the function. The lua functions os.time, which is defined by a luaTeX library, and context, which is defined by ConTeXt, needed to be accessed through a global name space. On the other hand, the math.randomseed function, which is part of lua, could be accessed as is.
A separate lua instance also makes debugging slightly easier. With \ctxlua the error message starts with
! LuaTeX error <main ctx instance>:
With \usercode the error message starts with
! LuaTeX error <private user instance>:
This makes it easier to narrow down the source of error.
Normally, it is best to define your lua functions in the user name space. If you are writing a module, then define your lua functions in the third instance and in a name space which is the name of your module. In this article, I will simply use the default lua instance, but take care to define all my lua functions in a userdata name space.
Now that we have some idea of how to work with luaTeX, let's look at some examples.
Arithmetic without using a abacus
Doing simple arithmetic in TeX can be extremely difficult, as illustrated by the division macro in the introduction. With lua, simple arithmetic becomes trivial. For example, if you want a macro to find the cosine of an angle (in degrees), you can write
\def\COSINE#1% {\ctxlua(context(math.cos(#1*2*pi/360))}
The built-in math.cos function assumes that the argument is specified in radians, so we convert from degrees to radians on the fly. If you want to type the value of $\pi$ in an article, you can simply say
$\pi = \ctxlua{context(math.pi)}$
or if you want less precision (notice the percent sign is escaped)
$\pi = \ctxlua{context("\%.6f", math.pi)}$
Loops without worrying about expansion
Loops in TeX are tricky because macro assignments and macro expansion interact in strange ways. For example, suppose we want to typeset a table showing the sum of the roll of two dice and want the output to look like this
\setupcolors[state=start] \setupTABLE[each][each][width=2em,height=2em,align={middle,middle}] \setupTABLE[r][1][background=color,backgroundcolor=gray] \setupTABLE[c][1][background=color,backgroundcolor=gray] \bTABLE \bTR \bTD $(+)$ \eTD \bTD 1 \eTD \bTD 2 \eTD \bTD 3 \eTD \bTD 4 \eTD \bTD 5 \eTD \bTD 6 \eTD \eTR \bTR \bTD 1 \eTD \bTD 2 \eTD \bTD 3 \eTD \bTD 4 \eTD \bTD 5 \eTD \bTD 6 \eTD \bTD 7 \eTD \eTR \bTR \bTD 2 \eTD \bTD 3 \eTD \bTD 4 \eTD \bTD 5 \eTD \bTD 6 \eTD \bTD 7 \eTD \bTD 8 \eTD \eTR \bTR \bTD 3 \eTD \bTD 4 \eTD \bTD 5 \eTD \bTD 6 \eTD \bTD 7 \eTD \bTD 8 \eTD \bTD 9 \eTD \eTR \bTR \bTD 4 \eTD \bTD 5 \eTD \bTD 6 \eTD \bTD 7 \eTD \bTD 8 \eTD \bTD 9 \eTD \bTD 10 \eTD \eTR \bTR \bTD 5 \eTD \bTD 6 \eTD \bTD 7 \eTD \bTD 8 \eTD \bTD 9 \eTD \bTD 10 \eTD \bTD 11 \eTD \eTR \bTR \bTD 6 \eTD \bTD 7 \eTD \bTD 8 \eTD \bTD 9 \eTD \bTD 10 \eTD \bTD 11 \eTD \bTD 12 \eTD \eTR \eTABLE
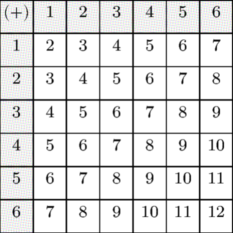
The tedious (but faster!) way to achieve this is to simply type the whole table by hand.
It is however natural to want to write this table as a loop, and compute the values. A first ConTeXt implementation using the recursion level might be:
\bTABLE \bTR \bTD $(+)$ \eTD \dorecurse{6} {\bTD \recurselevel \eTD} \eTR \dorecurse{6} {\bTR \bTD \recurselevel \eTD \edef\firstrecurselevel{\recurselevel} \dorecurse{6} {\bTD \the\numexpr\firstrecurselevel+\recurselevel \eTD}% \eTR} \eTABLE
However, this does not work as expected, yielding all zeros.
A natural table stores the contents of all the cells, before typesetting it. But it does not expand the contents of its cell before storing them. So, at the time the table is actually typeset, TeX has already finished the \dorecurse and \recurselevel is set to 0.
The solution is to place \expandafter at the correct location(s) to coax TeX into expanding the \recurselevel macro before the natural table stores the cell contents. The difficult part is figuring out the exact location of \expandafters. Here is a solution that works:
\bTABLE \bTR \bTD $(+)$ \eTD \dorecurse{6} {\expandafter \bTD \recurselevel \eTD} \eTR \dorecurse{6} {\bTR \edef\firstrecurselevel{\recurselevel} \expandafter\bTD \recurselevel \eTD \dorecurse{6} {\expandafter\bTD \the\numexpr\firstrecurselevel+\recurselevel \relax \eTD} \eTR} \eTABLE
We only needed to add three \expandafters to make the naive loop work. Nevertheless, finding the right location of \expandafter can be frustrating, especially for a non-expert.
By contrast, in luaTeX writing loops is easy. Once a lua instance starts, TeX does not see anything until the lua instance exits. So, we can write the loop in lua, and simply print the values that we would have typed to the TeX stream. When the control is passed to TeX, TeX sees the input as if we had typed it by hand. Consequently, macro expansion is no longer an issue. For example, we can get the above table by:
\startluacode context.bTABLE() context.bTR() context.bTD() context("$(+)$") context.eTD() for j=1,6 do context.bTD() context(j) context.eTD() end context.eTR() for i=1,6 do context.bTR() context.bTD() context(i) context.eTD() for j=1,6 do context.bTD() context(i+j) context.eTD() end context.eTR() end context.eTABLE() \stopluacode
The lua functions such as context.bTABLE() and context.bTR() are just abbreviations for running context ("\\bTABLE"), context("\\bTR"), etc. See the ConTeXt lua document manual for more details about such functions. The rest of the code is a simple nested for-loop that computes the sum of two dice. We do not need to worry about macro expansion at all!
Parsing input without exploding your~head
In order to get around the weird rules of macro expansion, writing a parser in TeX involves a lot of macro jugglery and catcode trickery. It is a black art, one of the biggest mysteries of TeX for ordinary users.
As an example, let's consider typesetting chemical molecules in TeX. Normally, molecules should be typeset in text mode rather than math mode. For example, 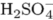 , can be input as
, can be input as H\low{2SO\lohi{4}{--}}. Typing so much markup can be cumbersome. Ideally, we want a macro such that we type \molecule{H_2SO_4^-} and the macro translates this into H\low{2SO\lohi{4}{--}}. Such a macro can be written in TeX as follows.
\newbox\chemlowbox \def\chemlow#1% {\setbox\chemlowbox \hbox{{\switchtobodyfont[small]#1}}} \def\chemhigh#1% {\ifvoid\chemlowbox \high{{\switchtobodyfont[small]#1}}% \else \lohi{\box\chemlowbox} {{\switchtobodyfont[small]#1}} \fi} \def\finishchem% {\ifvoid\chemlowbox\else \low{\box\chemlowbox} \fi} \unexpanded\def\molecule% {\bgroup \catcode`\_=\active \uccode`\~=`\_ \uppercase{\let~\chemlow}% \catcode`\^=\active \uccode`\~=`\^ \uppercase{\let~\chemhigh}% \dostepwiserecurse {65}{90}{1} {\catcode \recurselevel = \active \uccode`\~=\recurselevel \uppercase{\edef~{\noexpand\finishchem \rawcharacter{\recurselevel}}}}% \catcode`\-=\active \uccode`\~=`\- \uppercase{\def~{--}}% \domolecule }% \def\domolecule#1{#1\finishchem\egroup}
This monstrosity is a typical TeX parser. Appropriate characters need to be made active; occasionally, \lccode and \uccode need to be set; signaling tricks are needed (for instance, checking if \chemlowbox is void); and then magic happens (or so it seems to a flabbergasted user). More sophisticated parsers involve creating finite state automata, which look even more monstrous.
With luaTeX, things are different. luaTeX includes a general parser based on PEG (parsing expression grammar) called lpeg. This makes writing parsers in TeX much more comprehensible. For example, the above \molecule macro can be written as
\startluacode userdata = userdata or {} local lowercase = lpeg.R("az") local uppercase = lpeg.R("AZ") local backslash = lpeg.P("\\") local csname = backslash * lpeg.P(1) * (1-backslash)^0 local plus = lpeg.P("+") / "\\textplus " local minus = lpeg.P("-") / "\\textminus " local digit = lpeg.R("09") local sign = plus + minus local cardinal = digit^1 local integer = sign^0 * cardinal local leftbrace = lpeg.P("{") local rightbrace = lpeg.P("}") local nobrace = 1 - (leftbrace + rightbrace) local nested = lpeg.P {leftbrace * (csname + sign + nobrace + lpeg.V(1))^0 * rightbrace} local any = lpeg.P(1) local subscript = lpeg.P("_") local superscript = lpeg.P("^") local somescript = subscript + superscript local content = lpeg.Cs(csname + nested + sign + any) local lowhigh = lpeg.Cc("\\lohi{%s}{%s}") * subscript * content * superscript * content / string.format local highlow = lpeg.Cc("\\hilo{%s}{%s}") * superscript * content * subscript * content / string.format local low = lpeg.Cc("\\low{%s}") * subscript * content / string.format local high = lpeg.Cc("\\high{%s}") * superscript * content / string.format local justtext = (1 - somescript)^1 local parser = lpeg.Cs((csname + lowhigh + highlow + low + high + sign + any)^0) userdata.moleculeparser = parser function userdata.molecule(str) return parser:match(str) end \stopluacode \def\molecule#1% {\ctxlua{userdata.molecule("#1")}}
This is more verbose than the TeX solution, but is easier to read and write. With a proper parser, I do not have to use tricks to check if either one or both _ and ^ are present. More importantly, anyone (once they know the lpeg syntax) can read the parser and easily understand what it does. This is in contrast to the implementation based on TeX macro jugglery which require you to implement a TeX interpreter in your head to understand.
Conclusion
luaTeX is removing many TeX barriers: using system fonts, reading and writing Unicode files, typesetting non-Latin languages, among others. However, the biggest feature of luaTeX is the ability to use a high-level programming language to program TeX. This can potentially lower the learning curve for programming TeX.
In this article, I have mentioned only one aspect of programming TeX: macros that manipulate their input and output some text to the main TeX stream. Many other kinds of manipulations are possible: luaTeX provides access to TeX boxes, token lists, dimensions, glues, catcodes, direction parameters, math parameters, etc. The details can be found in the luaTeX manual.
- ↑ Not surprising, as two of luaTeX's main developers\Dash Taco Hoekwater and Hans Hagen\Dash are also the main ConTeXt developers.
- ↑ The output of
tex.print(...)is buffered and not passed to TeX until the lua instance has stopped. - ↑ In this example, I used two different kinds of quotations to avoid escaping quotes. Escaping quotes inside
\directluais tricky. The above was a contrived example; if you ever need to escape quotes, you can use the\startluacode ... \stopluacodesyntax explained later.